初始化

在运行整个里程计系统时，我们需要定义整个系统的初始状态（即初始的 $q$ 、 $p$ 、 $v$ 、 $b a$ 和 $b a$ ）。而初始状态则需要通过初始化进行计算。针对实际中的不同情况我们设计了静态初始化和动态初始化两种方案，通过IMU和视觉联合判断旋转哪一种方式进行初始化。在静态初始化中我们使用滑窗内IMU数据的平均值，并且通过施密特正交化恢复IMU姿态。而在动态初始化中我们通过视觉、状态和先验构造代价函数，通过优化的方式恢复初始状态。

静态初始化

静止初始化是指在视频序列开始阶段，需要有一段静止状态，系统利用静止状态的IMU数据来估计重力方向、加速度计陀螺仪biases。

静止初始化需要检测IMU的跳变过程（其中包含两个状态：静止状态、跳变状态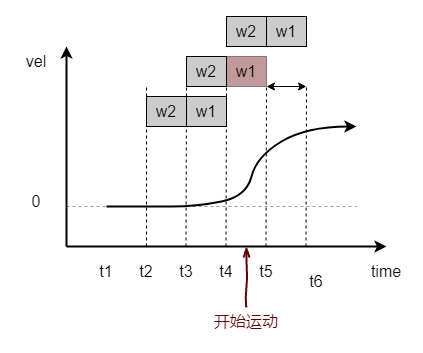）：在这里插入图片描述

计算初始旋转矩阵

使用施密特正交化计算： $_{W}^{I_{0}} R$

计算 $z$ 轴:

z = \frac{z}{z . n o r m ()} (1)

计算 $x$ 轴:

x = | z |^{\times} e_{1} (2)

其中, $e_{1} = [1, 0, 0]^{⊤}$

计算 $y$ 轴:

y = | z |^{\times} x (3)

可得：

_{W}^{I_{0}} R = [\begin{matrix} x^{⊤} & y^{⊤} & z^{⊤} \end{matrix}] (4)

计算陀螺仪bias

静止时刻的陀螺仪理想测量值（角速度）应该为0，因此陀螺仪的bias即窗口陀螺仪数据的平均值。

a v g_{w m} = \frac{1}{n} \sum_{1}^{n} w_{m} (5)

计算加速度计bias

静止时的加速度计bias为加速度平均值与实际重力加速度的差：

a v g_{a m} -_{W}^{I_{0}} R g (6)

$g$ 为世界系下的重力加速度，将重力矢量从世界系投影到IMU坐标系下。

动态初始化

构造线性约束计算初始[特征点位置，速度，重力]

利用帧变换的基本性质，可以将向量 $^{I_{i}} p_{f}$ ( $i$ 帧第 $j$ 个特征在IMU坐标系下的坐标)表示如下：

^{C_{i}} p_{j} =_{I}^{C} C_{I_{0}}^{I_{i}} C (^{I_{0}} p_{j} -^{I_{0}} p_{I_{i}}) +^{C} p_{I} (7)

通过位置计算公式将 $^{I_{0}} p_{I_{i}}$ 展开可得：

\begin{aligned} ^{C_{i}} p_{j} & =_{I}^{C} C_{I_{0}}^{I_{i}} C (^{I_{0}} p_{j} -^{I_{0}} v_{0} Δ t_{i} -^{I_{0}} g \frac{Δ t_{i}^{2}}{2} - s (t_{i})) +^{C} p_{I} (8) \end{aligned}

其中， $[^{I_{0}} p_{j},^{I_{0}} v_{0},^{I_{0}} g]$ 是想获得的系统部分初始状态。

通过相机投影公式：

z_{i j} = [\begin{matrix} u_{i j} \\ v_{i j} \end{matrix}] = [\begin{matrix} \frac{C_{i} x_{j}}{C_{i} z_{j}} \\ \frac{C_{i} y_{j}}{C_{i} z_{j}} \end{matrix}] (9) [\begin{matrix} 1 & 0 & - u_{i j} \\ 0 & 1 & - v_{i j} \end{matrix}]^{C_{i}} p_{j} = [\begin{matrix} 0 \\ 0 \end{matrix}] (10)

可将(8)式写成 $A_{i j} x = b_{i j}$ 的形式：

\begin{aligned} x & = {[\begin{array}{c} ^{I_{0}} p_{1}^{⊤} & \dots & ^{I_{0}} p_{M}^{⊤} & ^{I_{0}} v_{0}^{⊤} & ^{I_{0}} g^{⊤} \end{array}]}^{⊤} (11) \\ A_{i j} & = [\begin{array}{c} 1 & 0 & - u_{i j} \\ 0 & 1 & - v_{i j} \end{array}]_{I}^{C} C_{I_{0}}^{I_{i}} C T_{i j} (12) \\ b_{i j} & = [\begin{array}{c} 1 & 0 & - u_{i j} \\ 0 & 1 & - v_{i j} \end{array}] (_{I}^{C} C_{I_{0}}^{I_{i}} C s (t_{i}) -^{C} p_{I}) (13) \end{aligned}

其中，

T_{i j} = [\begin{matrix} \dots & I_{3} & \dots & - Δ t_{i} I_{3} & _{I_{i}}^{I_{0}} C_{C}^{I} C & - \frac{Δ t_{i}^{2}}{2} I_{3} \end{matrix}] (14)

至此已构造出线性约束，通过多项式的伴随矩阵和SVD分解可解出 $x$ 。

通过最大似然估计优化现有状态

通过施密特正交化计算出初始 $_{W}^{I_{0}} R$ 将 $x$ 的所有状态转换到全局坐标系{ $W$ }当中用于构建残差，用相机模型、IMU模型和先验因子构建代价函数，并将状态设置为优化参数进行优化。

相机模型：

\begin{aligned} z_{c, k} & = h_{c} (x) + n_{c, k} \\ = h_{d} (z_{n, k}, ζ) + n_{c, k} \\ = h_{d} (h_{p} (^{C_{k}} p_{f}), ζ) + n_{c, k} \\ = h_{d} (h_{p} (h_{t} (^{W} p_{f},_{W}^{C_{k}} R,^{W} p_{C_{k}})), ζ) + n_{c, k} \end{aligned} (15)

其中， $h_{d}$ 为相机畸变矫正， $h_{p}$ 为投影模型， $h_{t}$ 为坐标系变化（{G}->{C}）。

残差：

C_{C} ≜ {‖ z_{c} - h_{c} (x) ‖}_{R_{c}^{- 1}}^{2} (16)

IMU模型：

\begin{aligned} ^{W} p_{k + 1} & =^{W} p_{k} +^{W} v_{k} Δ t - \frac{1}{2}^{W} g Δ t^{2} +_{W}^{k} R^{⊤}^{k} α_{k + 1} (17) \\ ^{W} v_{k + 1} & =^{W} v_{k} -^{W} g Δ t +_{W}^{k} R^{⊤}^{k} β_{k + 1} (18) \\ _{W}^{k + 1} \bar{q} & =_{k}^{k + 1} \bar{q} \otimes_{W}^{k} \bar{q} (19) \end{aligned}

其中，

\begin{aligned} ^{k} α_{k + 1} & ≃^{k} {\overset{˘}{α}}_{k + 1} + \frac{\partial α}{\partial b_{a}} |_{{\bar{b}}_{a}} Δ b_{a} + \frac{\partial α}{\partial b_{w}} |_{{\bar{b}}_{w}} Δ b_{w} (20) \\ ^{k} β_{k + 1} & ≃^{k} {\overset{˘}{β}}_{k + 1} + \frac{\partial β}{\partial b_{a}} |_{{\bar{b}}_{a}} Δ b_{a} + \frac{\partial β}{\partial b_{w}} |_{{\bar{b}}_{w}} Δ b_{w} (21) \\ \begin{array}{c} _{k}^{k + 1} \end{array} \bar{q} & ≃ \bar{q} (Δ b_{w})^{- 1} \otimes_{k}^{k + 1} \overset{˘}{\bar{q}} (22) \end{aligned}

$^{k} {\overset{˘}{α}}_{k + 1},^{k} {\overset{˘}{β}}_{k + 1},_{k}^{k + 1} \overset{˘}{\bar{q}}$ 为当前估计偏置下与积分的测量值。

残差：

r_{I} (x) = [\begin{matrix} 2 vec (_{V}^{k + 1} \bar{q} \otimes_{V}^{k} {\bar{q}}^{- 1} \otimes_{k}^{k + 1} {\overset{˘}{q}}^{- 1} \otimes \bar{q} (Δ b_{w})) \\ b_{w, k + 1} - b_{w, k} \\ (\binom{_{V}^{k} R (^{V} v_{k + 1} -^{V} v_{k} +_{W}^{V} R^{W} g Δ t)}{-^{k} {\overset{˘}{β}}_{k + 1} - {\frac{\partial β}{\partial b_{a}} |}_{{\overset{―}{b}}_{a}} Δ b_{a} - {\frac{\partial β}{\partial b_{w}} |}_{{\overset{―}{b}}_{w}} Δ b_{w}}) \\ b_{a, k + 1} - b_{a, k} \\ (\binom{_{V}^{k} R (^{V} p_{k + 1} -^{V} p_{k} -^{V} v_{k} Δ t + \frac{1}{2}_{W}^{V} R^{W} g Δ t^{2})}{-^{k} {\overset{˘}{α}}_{k + 1} - {\frac{\partial α}{\partial b_{a}} |}_{{\overset{―}{b}}_{a}} Δ b_{a} - {\frac{\partial α}{\partial b_{w}} |}_{b_{w}} Δ b_{w}}) \end{matrix}] (23)

C_{I} ≜ ∥ 0 - r_{I} (x) ∥_{P^{- 1}}^{2} (24)

先验残差：

通过当前时间状态的线性化值和估计值构建残差：

C_{C} ≜ {‖ x ⊞ x_{l i n} ‖}_{Λ}^{2} (25)

最后进行优化，使残差达到最小值，

min_{x} \sum C_{I} + \sum C_{C} + \sum C_{P} (26)

当残差收敛，得到的优化参数为最终的初始状态，初始化结束。